主题:  How far in the regularity theory of the Navier-Stokes equations?主讲人:  Hugo Beirao da Veiga地点:  松江校区2号学院楼331理学院报告厅时间:  2018-10-18 15:00:00组织单位:   理学院应用数学系

主讲人简介：

Hugo Beirao da Veiga现为意大利比萨大学数学系教授，1971年获法国巴黎第六大学博士学位，师从G. Stampacchia教授，从事偏微分方程、泛函分析及数学流体力学理论的研究，尤其是在Navier-Stokes方程等流体力学方程的研究方面有诸多杰出的工作。在CPAM、ARMA、JMPA、ARMA等国际著名期刊上发表130多篇学术论文，是多家国际期刊的编委。

内容摘要：

The starting point of this talk is the well known sufficient condition for regularity of weak solutions to the evolution Navier-Stokes equations,sometimes called Prodi-Serrin's condition (PS condition).Roughly speaking,it establishes that solutions v which belong to the functional space   

,   

where    and     ,are regular. On the other hand,a formal equivalence   is suggested by the well known equation

.

In three papers published nearly twenty years ago we have proved some results which support this equivalence.In a recent paper we obtained new results in this direction.Interesting open problems still remain.

讲座主持：秦玉明 教授

讲座语言：英语

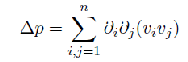撰写：秦玉明